Quante sono le possibili partite di scacchi?

Il gioco degli scacchi è un gioco da tavolo noto per la sua complessità e si può facilmente capire che il numero di possibili partite di scacchi è sicuramente grande con il seguente ragionamento alla Fermi.
Il Bianco ha 20 possibili mosse alla prima mossa, cui il Nero può replicare con 20 possibili mosse.
Questo porta allora a 20 x 20 = 202 = 400 possibili configurazioni dopo la prima mossa.
Questo numero di 20 mosse a disposizione per la prima mossa è limitato dal fatto che nella prima mossa solo i cavalli e i pedoni possono muoversi, ma dopo la prima mossa ( in dipendenza della scelta fatta dal giocatore) potranno muoversi altri pezzi con maggiore mobilità come Regina, Torri, Alfieri e Re, aumentando le possibili mosse.
Consideriamo allora per il momento un numero medio di mosse disponibili a mossa per colore di 20, una stima chiaramente bassa.
Consideriamo, inoltre, che sicuramente le partite di scacchi non possono durare per un numero di mosse infinito a causa delle regole della triplice ripetizione e delle 50 mosse.
Se consideriamo di avere partite di scacchi che durano 40 mosse, allora si ottiene un numero di possibili partite che è 20 moltiplicato per se stesso 2 x 40 = 80 volte (20 è il numero di mosse disponibili a mossa per colore), quindi è 2080 che è circa uguale a 10104, quindi un numero costituito da 1 seguito da 104 zeri.
Questa prima stima è però grossolana e al ribasso perché tiene conto di un numero medio di 20 possibili mosse ad ogni mossa di un colore, che è a sua volta un numero al ribasso per quanto discusso in precedenza.

Claude Shannon (in foto) è stato il primo a trovare una
Questi ultimi fatti ci dicono che la stima di Shannon è anch'essa una stima per difetto perché a scacchi è possibile non accordarsi per il pareggio in posizione pari o non arrendersi in posizione persa, quindi 40 è un numero di mosse per partita al ribasso.
Di conseguenza, Shannon mette assieme questi dati e, sfruttando il ragionamento illustrato prima, ottiene una stima che è 302x40 = 3080 che è circa 10120.
Nel suo articolo, Shannon fa questa stima per mostrare come per un computer un approccio alla risoluzione degli scacchi di “forza bruta” , ovvero calcolando tutte le possibili partite, non è molto praticabile.Lo stesso Shannon calcola che se anche un computer calcolasse una mossa ogni microsecondo (10 -6 secondi), allora calcolerebbe circa 3 x 1017 mosse all'anno, quindi calcolerebbe tutte le possibili varianti negli scacchi in circa
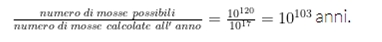
Questo è un numero gigantesco, soprattutto se confrontato con l'età del nostro Universo che è di circa 13,9 miliardi di anni, quindi nell'ordine di 10^{10} anni.
Un numero di anni di 10103 è 1093 volte l'età del nostro Universo.

Per esempio, tra le prime mosse possibili per il Bianco quattro di queste sono obiettivamente migliori delle altre (anche se le altre sono giocabili in partite tra umani) e in dipendenza della prima mossa del Bianco varia il numero di mosse sensate per il Nero e così via.
Se si considera sempre un numero medio di mosse a partita di 40 e che di solito per ogni mossa di un colore le migliori mosse a disposizione sono in media 3, si ottiene un numero di 32 x 40 che è circa 1038.
In questo caso, se un computer calcolasse una mossa sensata ogni microsecondo impiegherebbe “solo” 1021 anni.